In the previous post, we discussed how to quantize a neural network to half-precision floating point numbers and even 8 bits. This time, we will push the boundaries further by quantizing the network to integers, enabling us to further minimize the space it occupies. Let’s get started with some theory and then we will exercise it on a few examples.
Theory
Casting FP32 to INT8 can be performed in two ways: symmetric and asymmetric. In the asymmetric method, the range of the floating-point numbers is mapped to the range of integers, with the zero point shifting to the center of the range. This requires both a scaling factor and an offset. First, the offset is calculated as the difference between the center of the floating-point number range and the zero point. Then, the scaling factor is determined by the ratio of the floating-point number range to the integer range. Finally, the floating-point numbers are quantized to integers using this formula:
\(\text{INT8} = \text{Round}((\text{FP32} - \text{offset}) / \text{scaling factor})\) where \(\text{Round}\) represents the rounding function. INT8 is the integer representation of the floating-point number FP32. Below is a graphical representation of this process:
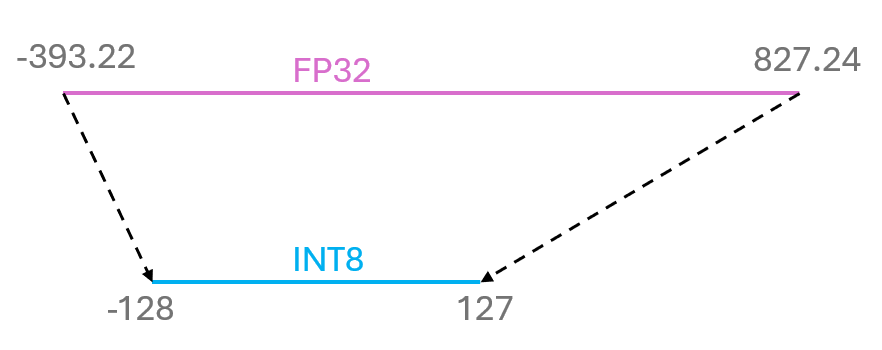
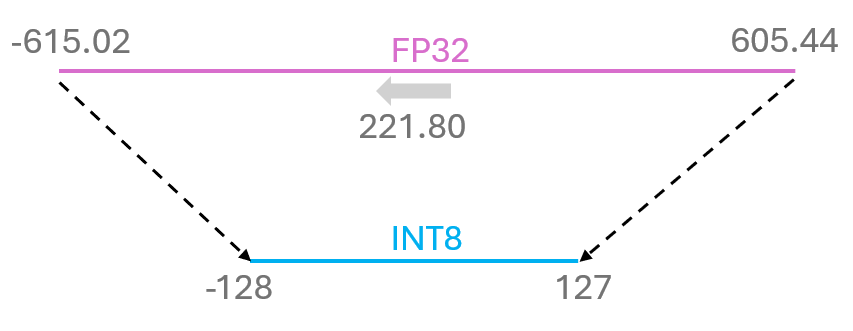
In this example, the offset is \(221.80\), and the scaling factor is \(4.767\). Therefore, two numbers are needed for the casting.
In symmetric quantization, there is no need for an offset. The scaling factor is calculated as the ratio of the FP32 to INT8 ranges or as the maximum absolute value of the floating-point numbers divided by the max of INT8. The formula for casting is:
\[\text{INT8} = \text{Round}(\text{max}(\text{abs}(\text{FP32})) / \text{scaling factor})\]Here is a graphical representation of symmetric quantization:
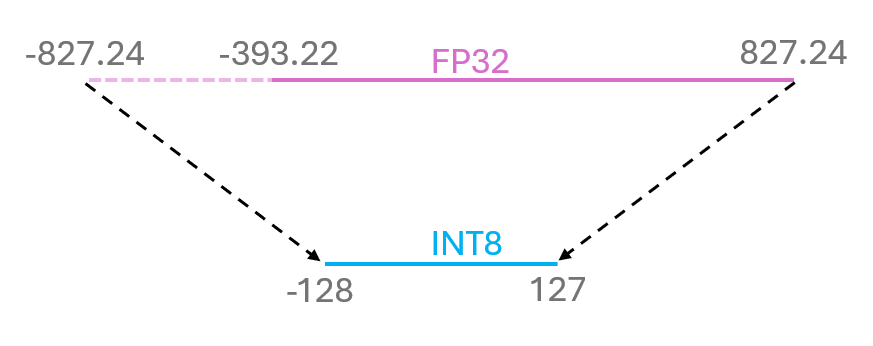
In this example, the scaling factor is \(6.463\). Thus, only one number is required for the casting.
Example with tensor
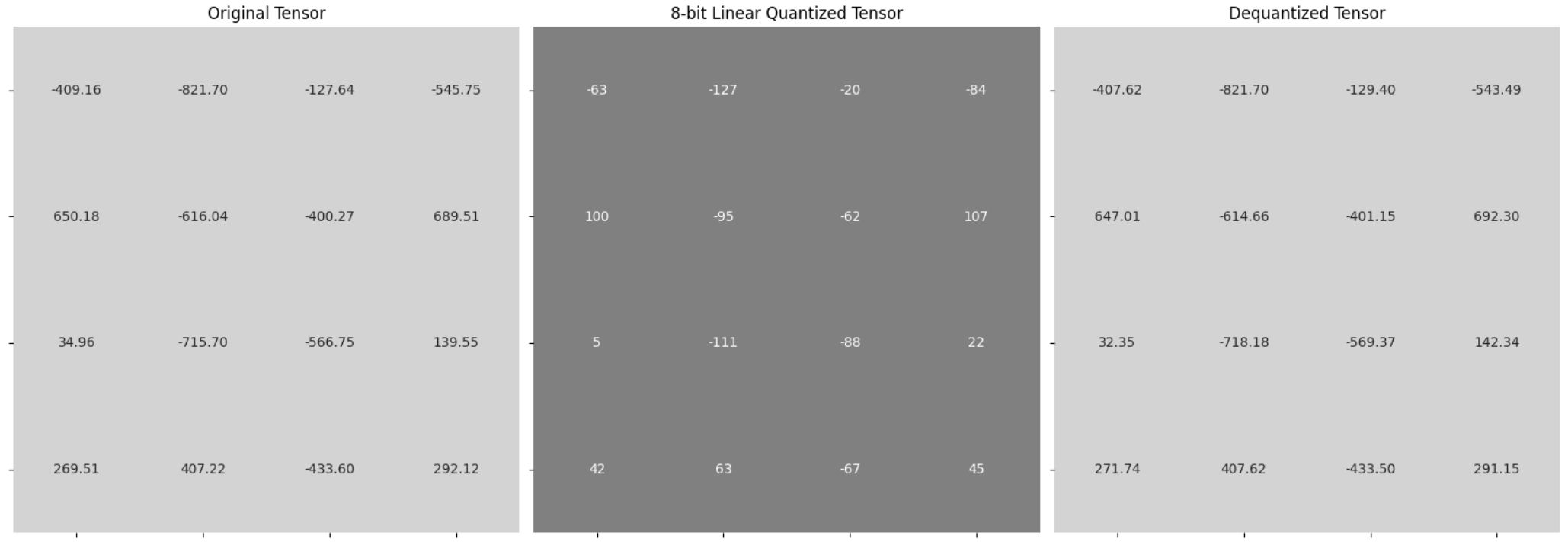
Let’s put this into practice. We will create a tensor \((4,4)\) with values in the range of \([-1000, 1000]\) and apply asymmetric casting. We will cast the FP32 tensor to the INT8 tensor and then back. Let’s first define a few functions that assist in the casting:
import torch
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
def get_q_scale_and_zero_point(tensor, dtype=torch.int8):
"""
A function that calculates the scale and zero point for quantization.
Args:
- tensor: The tensor to quantize
- dtype: The data type of the quantized tensor
"""
q_min, q_max = torch.iinfo(dtype).min, torch.iinfo(dtype).max
r_min, r_max = tensor.min().item(), tensor.max().item()
scale = (r_max - r_min) / (q_max - q_min)
zero_point = q_min - (r_min / scale)
if zero_point < q_min:
zero_point = q_min
elif zero_point > q_max:
zero_point = q_max
else:
zero_point = int(round(zero_point))
return scale, zero_point
def linear_q_with_scale_and_zero_point(tensor, scale, zero_point, dtype=torch.int8):
"""
A function that quantizes a tensor using a scale and zero point.
Args:
- tensor: The tensor to quantize
- scale: The scale of the quantized tensor
- zero_point: The zero point of the quantized tensor
- dtype: The data type of the quantized tensor
"""
scaled_and_shifted_tensor = tensor / scale + zero_point
rounded_tensor = torch.round(scaled_and_shifted_tensor)
q_min = torch.iinfo(dtype).min
q_max = torch.iinfo(dtype).max
q_tensor = rounded_tensor.clamp(q_min, q_max).to(dtype)
return q_tensor
def linear_dequantization(quantized_tensor, scale, zero_point):
return scale * (quantized_tensor.float() - zero_point)
Now, we can create the tensor and quantize it:
# Define the range
low = -1000.0
high = 1000.0
# Create a uniform distribution
uniform_dist = torch.distributions.uniform.Uniform(low, high)
# Sample from the distribution
original_tensor = uniform_dist.sample((4, 4))
scaling, offset = get_q_scale_and_zero_point(original_tensor)
quantized_tensor = linear_q_with_scale_and_zero_point(original_tensor, scaling, offset)
dequantized_tensor = linear_dequantization(quantized_tensor, scaling, offset)
plot_quantization_errors(original_tensor, quantized_tensor, dequantized_tensor)
Here is the graphical representation of tensors:

For the original and dequantized tensors, we can measure the absolute error (difference between the original and dequantized tensor):
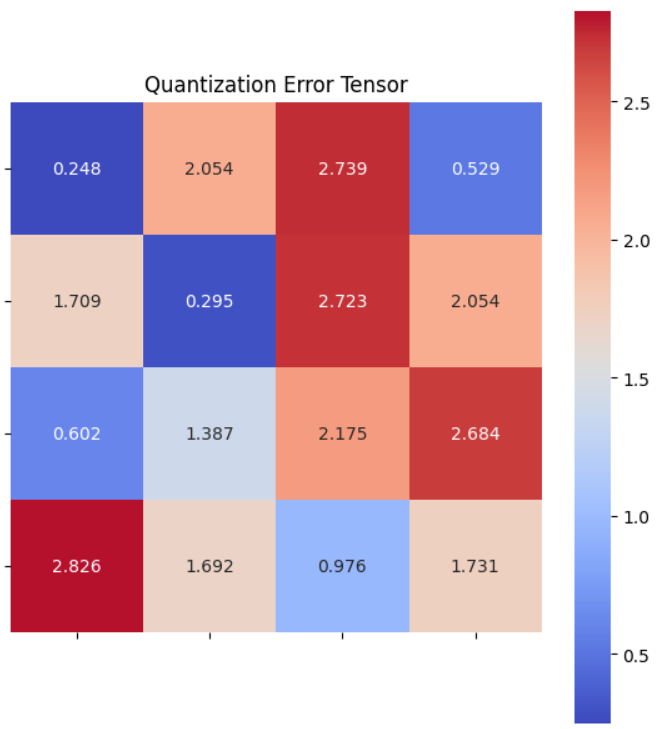
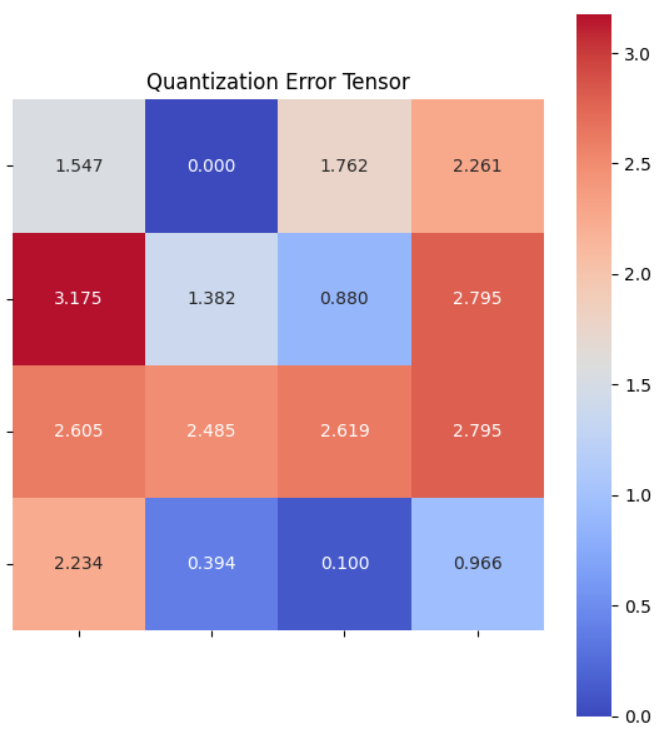
The error is quite small, less than \(1%\). Now, let’s perform the same operation with symmetric casting by defining additional functions:
def get_q_scale_symmetric(tensor, dtype=torch.int8):
"""
A function that calculates the scale for symmetric quantization.
Args:
- tensor: The tensor to quantize
- dtype: The data type of the quantized tensor
"""
r_max = tensor.abs().max().item()
q_max = torch.iinfo(dtype).max
# return the scale
return r_max / q_max
def linear_q_symmetric(tensor, dtype=torch.int8):
"""
A function that quantizes a tensor using symmetric quantization.
Args:
- tensor: The tensor to quantize
- dtype: The data type of the quantized tensor
"""
scale = get_q_scale_symmetric(tensor)
quantized_tensor = linear_q_with_scale_and_zero_point(
tensor,
scale=scale,
# in symmetric quantization zero point is = 0
zero_point=0,
dtype=dtype,
)
return quantized_tensor, scale
For the original and dequantized tensors, we can measure the absolute error:
To compare the two methods directly, we can calculate the mean squared error:
mse_asym = (dequantized_tensor - original_tensor).square().mean()
mse_sym = (dequantized_tensor_sym - original_tensor).square().mean()
print(f"MSE asymmetric: {mse_asym}")
print(f"MSE symmetric: {mse_sym}")
MSE asymmetric: 3.482797622680664
MSE symmetric: 4.056781768798828
The asymmetric casting results in a lower mean squared error because it accounts for the offset. However, the difference is not significant, and symmetric casting requires fewer parameters - only one number. This presents a trade-off between the two methods.
When higher precision is required, you can adjust the granularity of the quantization.
Granularity
As we have observed, it is possible to use a single number to quantize the entire tensor. However, when dealing with large tensors with vast value ranges, precision naturally diminishes. Here’s an example of how Mean Squared Error (MSE) increases with an increase in either the size of the tensor or the size of the range. Let’s further explore these dependencies, where each data point averaged over 100 tensors.
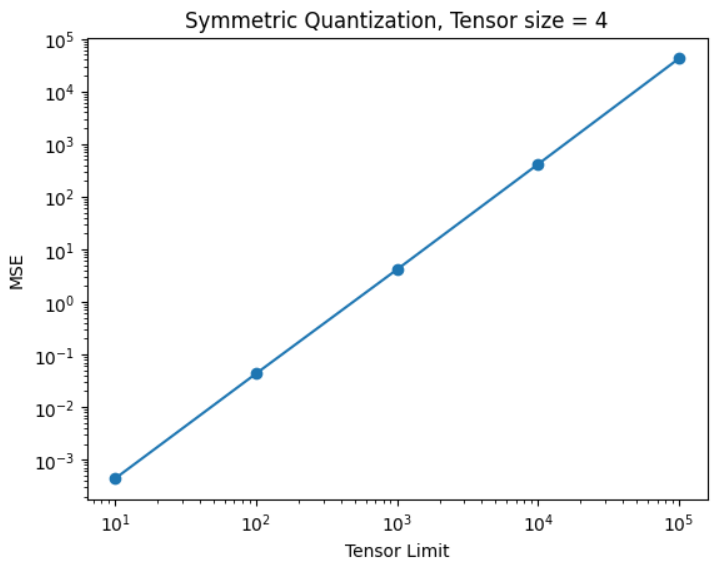
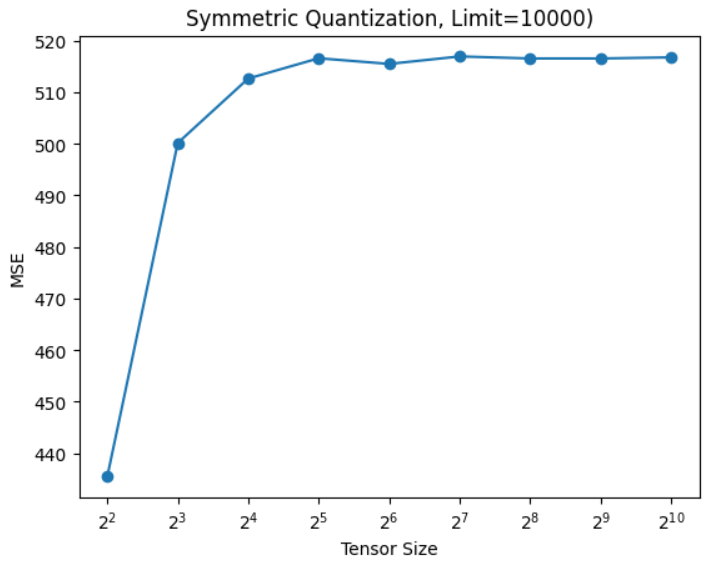
Instead of using a single number for the entire tensor, precision can be enhanced by employing multiple numbers. This concept is called granularity, where the tensor is divided into smaller parts, and each part undergoes separate casting. This approach improves precision. For example, casting can be done on a per-channel basis or even per group. Below is a visual representation of these approaches:

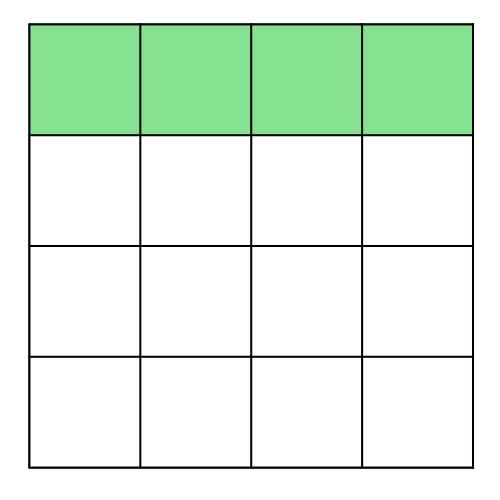
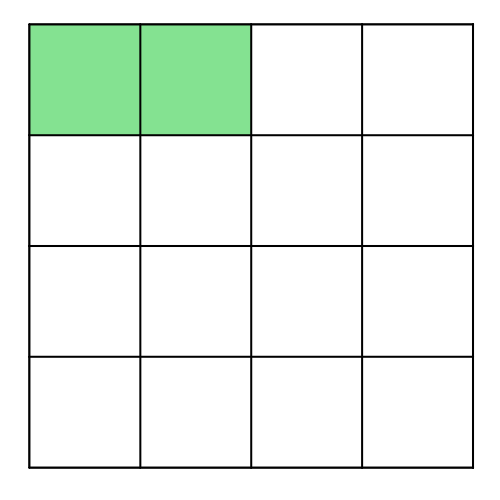
Finer granularity results in higher precision, but it also requires more numbers for casting. This balance between precision and resource requirements needs to be weighed. Let’s compare MSE for the various cases by defining the following functions:
def linear_q_symmetric_per_channel(r_tensor, dim, dtype=torch.int8):
"""
A function that quantizes a tensor per channel.
Args:
- r_tensor: The tensor to quantize
- dim: The dimension to quantize along
- dtype: The data type of the quantized tensor
"""
output_dim = r_tensor.shape[dim]
# store the scales
scale = torch.zeros(output_dim)
for index in range(output_dim):
sub_tensor = r_tensor.select(dim, index)
scale[index] = get_q_scale_symmetric(sub_tensor, dtype=dtype)
# reshape the scale
scale_shape = [1] * r_tensor.dim()
scale_shape[dim] = -1
scale = scale.view(scale_shape)
quantized_tensor = linear_q_with_scale_and_zero_point(
r_tensor, scale=scale, zero_point=0, dtype=dtype
)
return quantized_tensor, scale
def linear_q_symmetric_per_group(tensor, group_size, dtype=torch.int8):
"""
A function that quantizes a tensor per group.
Args:
- tensor: The tensor to quantize
- group_size: The size of the group
- dtype: The data type of the quantized tensor
"""
t_shape = tensor.shape
assert t_shape[1] % group_size == 0
assert tensor.dim() == 2
tensor = tensor.view(-1, group_size)
quantized_tensor, scale = linear_q_symmetric_per_channel(tensor, dim=0, dtype=dtype)
quantized_tensor = quantized_tensor.view(t_shape)
return quantized_tensor, scale
def linear_dequantization_per_group(quantized_tensor, scale, group_size):
"""
A function that dequantizes a quantized tensor per group.
Args:
- quantized_tensor: The quantized tensor
- scale: The scale of the quantized tensor
- group_size: The size of the group
"""
q_shape = quantized_tensor.shape
quantized_tensor = quantized_tensor.view(-1, group_size)
dequantized_tensor = linear_dequantization(quantized_tensor, scale, 0)
dequantized_tensor = dequantized_tensor.view(q_shape)
return dequantized_tensor
def quantization_error(original_tensor, dequantized_tensor):
"""
A function that calculates the quantization error between the original tensor and the dequantized tensor.
Args:
- original_tensor: The original tensor
- dequantized_tensor: The dequantized tensor
"""
return (original_tensor - dequantized_tensor).square().mean()
Now, we can cast the tensor using granularity per tensor, per channel, and per group:
limit = 1000
uniform_dist = torch.distributions.uniform.Uniform(-limit, limit)
original_tensor = uniform_dist.sample((64, 64))
# per tensor
quantized_tensor_per_matrix, scaling_per_matrix = linear_q_symmetric(original_tensor)
dequantized_tensor_per_matrix = linear_dequantization(
quantized_tensor_per_matrix, scaling_per_matrix, 0
)
# per channel
quantized_tensor_per_channel, scale_per_channel = linear_q_symmetric_per_channel(original_tensor, dim=0)
dequantized_tensor_per_channel = linear_dequantization(quantized_tensor_per_channel, scale_per_channel, 0)
# per group
quantized_tensor_per_group, scaling_per_group = linear_q_symmetric_per_group(
original_tensor, group_size=8
)
dequantized_tensor_per_group = linear_dequantization_per_group(
quantized_tensor_per_group, scaling_per_group, group_size=8
)
# print 3 errors
mse_per_matrix = quantization_error(original_tensor, dequantized_tensor_per_matrix)
mse_per_channel = quantization_error(original_tensor, dequantized_tensor_per_channel)
mse_per_group = quantization_error(original_tensor, dequantized_tensor_per_group)
print(f"MSE for per matrix quantization: {mse_per_matrix}")
print(f"MSE for per channel quantization: {mse_per_channel}")
print(f"MSE for per group quantization: {mse_per_group}")
And the output is:
MSE for per matrix quantization: 5.178160667419434
MSE for per channel quantization: 4.908818244934082
MSE for per group quantization: 3.649305582046509
Example with a neural network
For demonstration, we will use an encoder-decoder transformer, detr-resnet-50, for object detection. We will quantize the network to INT8 using symmetric casting and compare the results with the original model predictions. First, let’s define functions to quantize the network:
def w8_a16_forward(weight, input_data, scales, bias=None):
"""
A function that performs the forward pass of a linear layer with 8-bit weights and 16-bit scales.
Args:
- weight: The quantized weights of the linear layer
- input: The input tensor
- scales: The scales of the linear layer
- bias: The bias of the linear layer
"""
casted_weights = weight.to(input_data.dtype)
output = torch.nn.functional.linear(input_data, casted_weights) * scales
if bias is not None:
output = output + bias
return output
class W8A16LinearLayer(torch.nn.Module):
"""
A class that implements a linear layer with 8-bit weights and 16-bit scales.
The class initializes the weights and scales randomly and quantizes the weights
during initialization.
The forward pass of the layer uses the quantized weights and scales to compute the output.
"""
def __init__(self, in_features, out_features, bias=True, dtype=torch.float32):
super().__init__()
self.register_buffer(
"int8_weights",
torch.randint(-128, 127, (out_features, in_features), dtype=torch.int8),
)
self.register_buffer("scales", torch.randn((out_features), dtype=dtype))
if bias:
self.register_buffer("bias", torch.randn((1, out_features), dtype=dtype))
else:
self.bias = None
def quantize_weights(self, weights):
w_fp32 = weights.clone().to(torch.float32)
scales = w_fp32.abs().max(dim=-1).values / 127
scales = scales.to(weights.dtype)
int8_weights = torch.round(weights / scales.unsqueeze(1)).to(torch.int8)
self.int8_weights = int8_weights
self.scales = scales
def quantize_activations(self, activations):
a_fp32 = activations.clone().to(torch.float32)
scale = a_fp32.abs().max() / 127
scale = scale.to(activations.dtype)
int8_activations = torch.round(activations / scale).to(torch.int8)
self.int8_x = int8_activations
self.act_scale = scale
def quantize(self, weights):
w_fp32 = weights.clone().to(torch.float32)
scales = w_fp32.abs().max(dim=-1).values / 127
scales = scales.to(weights.dtype)
int8_weights = torch.round(weights / scales.unsqueeze(1)).to(torch.int8)
self.int8_weights = int8_weights
self.scales = scales
def forward(self, x):
return w8_a16_forward(self.int8_weights, x, self.scales, self.bias)
def replace_linear_with_target_and_quantize(
module, target_class, module_name_to_exclude
):
"""
A function that replaces all instances of nn.Linear in a module with a target class
and quantizes the weights.
Args:
- module: The module to replace the linear layers in
- target_class: The target class to replace the linear layers with
- module_name_to_exclude: The names of the modules to exclude from replacement
"""
for name, child in module.named_children():
if isinstance(child, torch.nn.Linear) and not any(
[x == name for x in module_name_to_exclude]
):
old_bias = child.bias
old_weight = child.weight
new_module = target_class(
child.in_features,
child.out_features,
old_bias is not None,
child.weight.dtype,
)
setattr(module, name, new_module)
getattr(module, name).quantize(old_weight)
if old_bias is not None:
getattr(module, name).bias = old_bias
else:
# Recursively call the function for nested modules
replace_linear_with_target_and_quantize(
child, target_class, module_name_to_exclude
)
# colors for visualization
COLORS = [
[0.000, 0.447, 0.741],
[0.850, 0.325, 0.098],
[0.929, 0.694, 0.125],
[0.494, 0.184, 0.556],
[0.466, 0.674, 0.188],
[0.301, 0.745, 0.933],
]
def plot_results(model, pil_img, results):
"""
A function that plots the results of object detection on an image.
Args:
- model: The model used for object detection
- pil_img: The PIL image to plot
- results: The results of object detection
"""
plt.figure(figsize=(16, 10))
plt.imshow(pil_img)
ax = plt.gca()
scores, labels, boxes = results["scores"], results["labels"], results["boxes"]
colors = COLORS * 100
for score, label, (xmin, ymin, xmax, ymax), c in zip(
scores.tolist(), labels.tolist(), boxes.tolist(), colors
):
ax.add_patch(
plt.Rectangle(
(xmin, ymin), xmax - xmin, ymax - ymin, fill=False, color=c, linewidth=3
)
)
text = f"{model.config.id2label[label]}: {score:0.2f}"
ax.text(xmin, ymin, text, fontsize=15, bbox=dict(facecolor="yellow", alpha=0.5))
plt.axis("off")
plt.show()
def fetch_image(image_url):
"""
A function that fetches an image from a URL and returns it as a PIL image.
Args:
- image_url: The URL of the image to fetch
"""
image = Image.open(requests.get(image_url, stream=True).raw).convert("RGB")
return image
Next, let’s download the model from Hugging Face. Remember to add your HF_TOKEN when running the notebook.
model_name = "facebook/detr-resnet-50"
device = torch.device("cpu")
#device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# you can specify the revision tag if you don't want the timm dependency
processor = DetrImageProcessor.from_pretrained(model_name, revision="no_timm")
model = DetrForObjectDetection.from_pretrained(model_name, revision="no_timm")
original_memory_footprint = model.get_memory_footprint()
print("Footprint of the model in MBs: ", original_memory_footprint / 1e6)
Footprint of the model in MBs: 166.524032
Let’s now download the image:
img_path ="https://cdn.pixabay.com/photo/2020/08/25/18/29/workplace-5517762_1280.jpg"
image = fetch_image(img_path).convert("RGB")
image

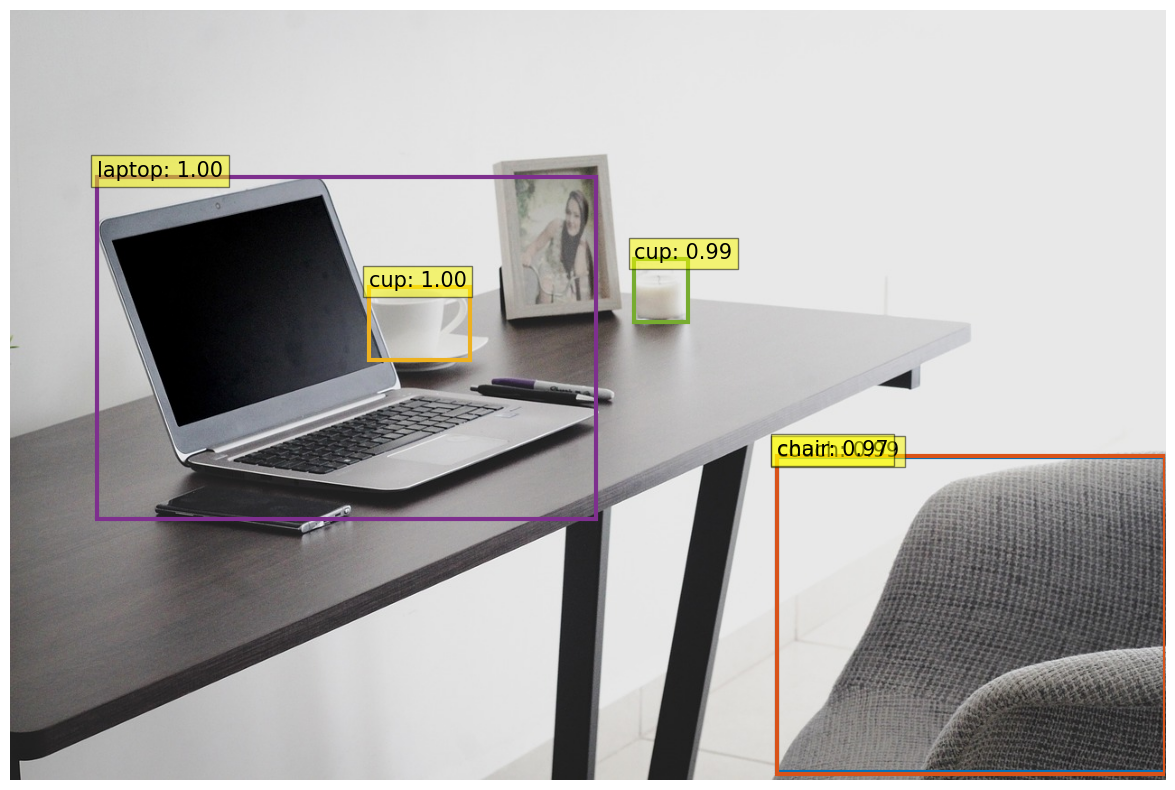
Now, let’s perform object detection:
inputs = processor(images=image, return_tensors="pt")
with torch.no_grad():
outputs = model(**inputs)
# convert outputs (bounding boxes and class logits) to COCO API
# let's only keep detections with score > 0.9
target_sizes = torch.tensor([image.size[::-1]])
results = processor.post_process_object_detection(
outputs, target_sizes=target_sizes, threshold=0.95
)[0]
plot_results(model, image, results)
Next, we quantize the model and perform object detection again:
quantized_model = deepcopy(model).to(device).half()
replace_linear_with_target_and_quantize(
quantized_model,
W8A16LinearLayer,
module_name_to_exclude=["0", "1", "2", "class_labels_classifier"],
)
inputs = processor(images=image, return_tensors="pt")
inputs = {
k: v.to(torch.float16) for k, v in inputs.items()
} # Convert inputs to half precision
with torch.no_grad():
outputs = quantized_model(**inputs)
# convert outputs (bounding boxes and class logits) to COCO API
# let's only keep detections with score > 0.9
target_sizes = torch.tensor([image.size[::-1]])
results = processor.post_process_object_detection(
outputs, target_sizes=target_sizes, threshold=0.95
)[0]
quantized_memory_footprint = quantized_model.get_memory_footprint()
print(
"Footprint of the quantized int8 model in MBs: ", quantized_memory_footprint / 1e6
)
plot_results(quantized_model, image, results)
Footprint of the quantized int8 model in MBs: 66.052672

The memory footprint of the quantized model is significantly smaller than that of the original model:
quantized_memory_footprint / original_memory_footprint
0.3966554929441055
The quantized model occupies approximately 40% of the original model’s space, yet the object detection results remain nearly identical. This is an excellent technique for reducing a model’s memory footprint without sacrificing much accuracy.
Conclusion
In this post, we explored how to quantize a neural network to integers. We covered symmetric and asymmetric casting, as well as calculating the scaling factor and offset. We also delved into the granularity of casting and its impact on precision. We demonstrated quantization on a tensor and a neural network, noting that the quantized model had a significantly smaller memory footprint than the original, with negligible differences in object detection results. This offers a great approach to minimizing a model’s memory footprint while maintaining accuracy. In our next post, we’ll discuss quantizing networks to binary numbers.
Importantly, pre-quantized models are readily available on Hugging Face, allowing you to use them directly without the need for self-quantization. However, understanding the mechanics can enhance one’s comprehension of what happens behind the scenes.
For the convenience of the reader, the full code can be found in the Google colab notebook.
I hope you enjoyed this post and learned something new. If you have any questions or suggestions, feel free to connect with me on LinkedIn. Thank you for reading!
